Efficient minimization of new quadric metric for simplifying meshes with appearance attributes

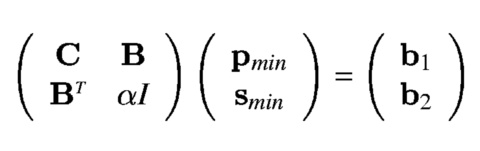
Abstract: In an earlier paper we introduced a new quadric metric for simplifying triangle meshes using the edge collapse operation. The quadric measures both the geometric accuracy of the simplified mesh surface and the fidelity of appearance fields defined on the surface (such as normals or colors). The minimization of this quadric metric involves solving a linear system of size (3+m)×(3+m), where m is the number of distinct appearance attributes. The system has only O(m) nonzero entries, so it can be solved in O(m²) time using traditional sparse solvers such as the method of conjugate gradients. In this short addendum, we show that the special structure of the sparsity permits the system to be solved in O(m) time.